Factor models are mathematical frameworks that describe the relationship between a set of observable variables and a smaller number of underlying factors. These models help explain variations in data and facilitate a better understanding of complex systems or phenomena. Factor models have various applications across disciplines, including finance, economics, marketing, psychology, and medicine. They can be used for portfolio optimization, risk management, forecasting, performance attribution, and data analysis. Factor models offer benefits such as simplifying complex relationships, improving forecasting, and identifying hidden patterns in data. However, they also have limitations, including potential model misspecification, data quality issues, and the risk of overfitting. Macroeconomic factor models use macroeconomic variables, such as interest rates or inflation, to explain variations in financial asset returns. These models help investors understand the impact of macroeconomic factors on their portfolios and make informed investment decisions. Fundamental factor models focus on firm-specific characteristics, such as earnings or market capitalization, to explain asset returns. These models are widely used in finance, especially for portfolio construction, risk management, and performance attribution. Statistical factor models use statistical techniques, such as principal component analysis (PCA) or factor analysis, to identify and estimate factors. These models are data-driven and aim to reduce dimensionality while capturing the underlying structure of the data. Hybrid factor models combine elements from different types of factor models, such as macroeconomic and fundamental factors. These models seek to capitalize on the strengths of multiple-factor models and provide a more comprehensive understanding of asset returns. Factor identification involves selecting the appropriate factors that are believed to explain the variations in the observable variables. This process is crucial, as the choice of factors can significantly impact the model's performance and accuracy. Factor estimation is the process of determining the weights or loadings of each factor on the observable variables. Various statistical techniques, such as regression analysis or PCA, can be used to estimate these factor loadings. Model specification involves defining the functional form and structure of the factor model. This includes determining the number of factors, the relationship between factors and observable variables, and any additional assumptions or constraints. Model validation is the process of evaluating the accuracy and reliability of a factor model. This involves testing the model on historical data or out-of-sample data and comparing its performance to alternative models or benchmarks. Factor models play a crucial role in portfolio construction and optimization, helping investors identify assets with desired factor exposures and diversify their portfolios to reduce risk and enhance returns. Factor models assist in risk management by providing insights into the sources of portfolio risk and identifying potential areas of vulnerability. By understanding factor exposures, investors can make informed decisions to mitigate risks and manage their portfolios effectively. Performance attribution involves analyzing the sources of portfolio returns and attributing them to specific factors. Factor models enable investors to determine which factors have contributed positively or negatively to their portfolio performance and adjust their strategies accordingly. Factor models can be used to forecast future asset returns and conduct scenario analysis. By incorporating historical data and factor relationships, these models help investors make informed predictions about the potential impact of various market conditions on their portfolios. Factor models are widely used in economics to study the relationships between economic variables, such as GDP growth, inflation, and unemployment. They help economists identify the driving forces behind economic fluctuations and assess the impact of policy changes on economic outcomes. In marketing, factor models are employed to analyze consumer behavior, segment markets, and develop targeted marketing strategies. These models can uncover underlying patterns in consumer preferences and provide insights into the factors that influence purchasing decisions. Factor models play a significant role in psychology, particularly in developing and validating psychological tests and scales. They help researchers identify and quantify latent traits or factors that underlie observed behaviors, such as personality traits or cognitive abilities. In medicine, factor models are used to analyze complex medical data and identify underlying factors contributing to disease progression or treatment outcomes. They can help researchers better understand the relationships between various risk factors, biomarkers, and clinical outcomes, leading to improved patient care. Model misspecification occur when a factor model's chosen factors, functional form, or assumptions do not accurately represent the underlying relationships. Misspecified models can lead to biased or inconsistent estimates, affecting the reliability and accuracy of the model. The performance of factor models depends heavily on the quality and availability of the data used. Inaccurate, incomplete, or outdated data can lead to erroneous conclusions and limit the model's effectiveness in explaining observed variations. Overfitting occurs when a factor model captures the noise in the data rather than the underlying relationships. Overfit models may perform well on the sample data but fail to generalize to new, unseen data, leading to poor predictive performance. Non-stationarity and structural breaks refer to changes in the underlying relationships between factors and observable variables over time. These changes can reduce the effectiveness of factor models in capturing the true relationships and pose challenges in forecasting and decision-making. Factor models have become essential tools across various disciplines, providing valuable insights into complex relationships and enabling data-driven decision-making. They have significantly contributed to finance, economics, marketing, psychology, and medicine advancements. Given the dynamic nature of real-world phenomena, ongoing research and model improvement are crucial for maintaining the relevance and accuracy of factor models. New techniques and methodologies continue to emerge, enhancing the ability of factor models to capture and explain complex relationships. While factor models provide valuable insights, it is essential to emphasize the role of human judgment in interpreting and applying the results. Experts must consider the limitations and assumptions of these models, combining their insights with domain knowledge and professional experience. As factor models become increasingly sophisticated and complex, seeking professional wealth management services can be highly beneficial. These experts can help navigate the challenges associated with factor models, tailor strategies to individual goals, and provide ongoing support to optimize investment decisions and financial outcomes.What Are Factor Models?
Types of Factor Models
Macroeconomic Factor Models
Fundamental Factor Models
Statistical Factor Models
Hybrid Factor Models

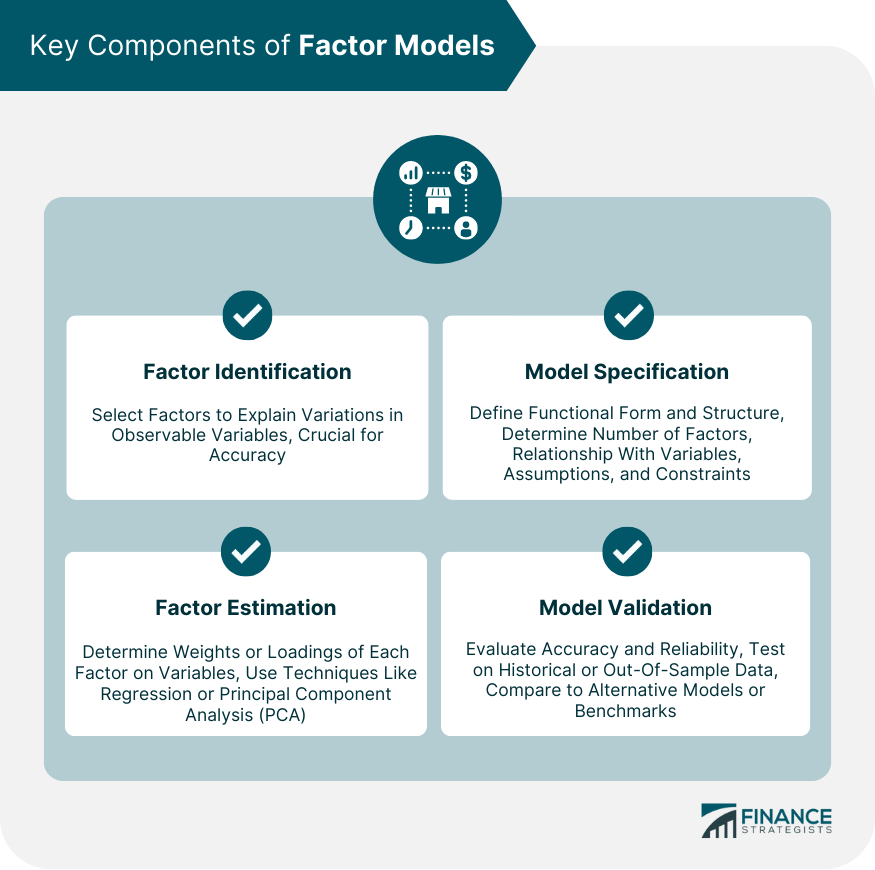
Key Components of Factor Models
Factor Identification
Factor Estimation
Model Specification
Model Validation
Applications of Factor Models in Finance
Portfolio Construction and Optimization
Risk Management
Performance Attribution
Forecasting and Scenario Analysis
Applications of Factor Models in Other Disciplines
Economics
Marketing
Psychology
Medicine
Challenges and Limitations of Factor Models

Model Misspecification
Data Quality and Availability
Overfitting
Non-stationarity and Structural Breaks
Final Thoughts
Factor Models FAQs
Factor models are mathematical frameworks that describe the relationship between a set of observable variables and a smaller number of underlying factors. These models help explain variations in data and facilitate a better understanding of complex systems or phenomena.
The key components of factor models include factor identification, factor estimation, model specification, and model validation. These components are crucial for building and validating accurate factor models.
Factor models have various applications in finance, including portfolio construction and optimization, risk management, performance attribution, and forecasting and scenario analysis. These models help investors make informed decisions and manage their portfolios effectively.
Factor models have limitations, including potential model misspecification, data quality issues, overfitting, and non-stationarity and structural breaks. These challenges can affect the reliability and accuracy of the models.
Factor models are widely used in other disciplines, such as economics, marketing, psychology, and medicine. In these fields, they help researchers identify and quantify latent factors underlying observed behaviors, analyze consumer behavior, and study relationships between economic variables and health outcomes.
True Tamplin is a published author, public speaker, CEO of UpDigital, and founder of Finance Strategists.
True is a Certified Educator in Personal Finance (CEPF®), author of The Handy Financial Ratios Guide, a member of the Society for Advancing Business Editing and Writing, contributes to his financial education site, Finance Strategists, and has spoken to various financial communities such as the CFA Institute, as well as university students like his Alma mater, Biola University, where he received a bachelor of science in business and data analytics.
To learn more about True, visit his personal website or view his author profiles on Amazon, Nasdaq and Forbes.















