The Binomial Option Pricing Model is a widely used method for valuing options, which are financial instruments that give the holder the right, but not the obligation, to buy or sell an underlying asset at a specified price on or before a specified date. The Binomial Option Pricing Model is a mathematical technique that estimates the value of an option by simulating potential price movements of the underlying asset. It uses a decision-tree approach to determine the option's value at each possible future point in time. Three key components of the Binomial Option Pricing Model are the binomial tree, risk-neutral probabilities, and backward induction. The binomial tree represents the possible price movements of the underlying asset, risk-neutral probabilities are used to calculate expected payoffs, and backward induction calculates the option's value at each node. The Binomial Option Pricing Model is applicable to various types of options, including European, American, and exotic options. However, it has limitations, such as requiring a large number of time steps for accurate results and its reliance on certain assumptions. The Binomial Option Pricing Model relies on several key assumptions and parameters that must be defined in order to accurately value an option. In the risk-neutral valuation approach, the model assumes that investors are indifferent to risk. This simplifies calculations, as expected returns are equal to the risk-free rate. The model divides the time until the option's expiration into discrete, equal intervals. This assumption allows for a clear representation of potential price movements and simplifies calculations. The model assumes that the underlying asset's price can either move up or down at each time step. This assumption simplifies the decision tree and makes calculations more manageable. The model assumes a constant, risk-free interest rate throughout the option's life. Additionally, the time between each step is assumed to be the same, which helps ensure consistency in calculations. The Binomial Option Pricing Model involves several key steps to accurately determine the value of an option. The binomial tree is a visual representation of possible stock price movements over time. It is constructed by dividing the time to expiration into equal intervals and calculating the possible stock prices at each node. At the end of the binomial tree, the option's value is determined by comparing its strike price to the underlying asset's price. This comparison results in either a positive payoff or zero, depending on whether the option is in or out of the money. Risk-neutral probabilities are used to calculate the expected payoffs at each node in the tree. These probabilities are calculated based on the risk-free interest rate, stock price movements, and time between steps. Backward induction is the process of working backward through the binomial tree to determine the option's value at each node. The expected payoffs at each node are discounted back to the present, resulting in the option's current value. The Binomial Option Pricing Model can be used to value various types of options, each with its own unique characteristics and rules. European options can only be exercised at their expiration date. The Binomial Option Pricing Model can accurately value these options by considering the potential payoffs at the option's expiration. American options can be exercised at any time before their expiration date. The Binomial Option Pricing Model can value these options by considering the optimal exercise strategy and incorporating early exercise possibilities at each node in the tree. Exotic options have unique features or conditions not found in standard options. The Binomial Option Pricing Model can be adapted to value these options by incorporating their specific rules and characteristics into the model's calculations. Several other models are used to value options, each with its own strengths and weaknesses. The Black-Scholes Model is a closed-form solution for option pricing that is widely used for European options. It is generally faster and easier to implement than the Binomial Option Pricing Model but cannot accommodate early exercise features of American options. Monte Carlo Simulation is a numerical technique that uses random sampling to estimate option prices. It can handle complex option structures and path-dependent features, but its accuracy depends on the number of simulations and can be computationally intensive. The Finite Difference Method is a numerical technique that solves partial differential equations to estimate option prices. It is more flexible than the Black-Scholes Model but can be more complex and computationally intensive compared to the Binomial Option Pricing Model. The Binomial Option Pricing Model has numerous practical applications and limitations that impact its use in the finance industry. The model is widely used by financial professionals, including traders, risk managers, and option pricing analysts, to value and analyze various types of options for investment and risk management purposes. The Binomial Option Pricing Model helps inform financial decision-making by providing accurate option valuations, allowing investors to better understand the potential risks and rewards associated with different strategies. Some limitations of the model include its reliance on certain assumptions, the need for a large number of time steps for accurate results, and its inability to perfectly replicate real-world market behavior. These limitations can affect the model's accuracy and applicability to certain situations. The Binomial Option Pricing Model is a widely used method for valuing options that estimates the value of an option by simulating potential price movements of the underlying asset. The model relies on several key assumptions and parameters that must be defined to accurately value an option, including risk-neutral valuation, discrete time steps, stock price movements, interest rates, and time. The model involves several key steps, including building the binomial tree, option valuation at maturity, risk-neutral probabilities, and backward induction. The Binomial Option Pricing Model can be used to value various types of options, including European, American, and exotic options, and is widely used by financial professionals for investment and risk management purposes. However, the model has some limitations, including its reliance on certain assumptions, the need for a large number of time steps for accurate results, and its inability to perfectly replicate real-world market behavior. Overall, the Binomial Option Pricing Model is a valuable tool for financial decision-making, but its limitations should be taken into account when using it to value options.What Is the Binomial Option Pricing Model?
Assumptions and Parameters of the Binomial Option Pricing Model
Risk-Neutral Valuation
Discrete Time Steps
Stock Price Movements
Interest Rates and Time
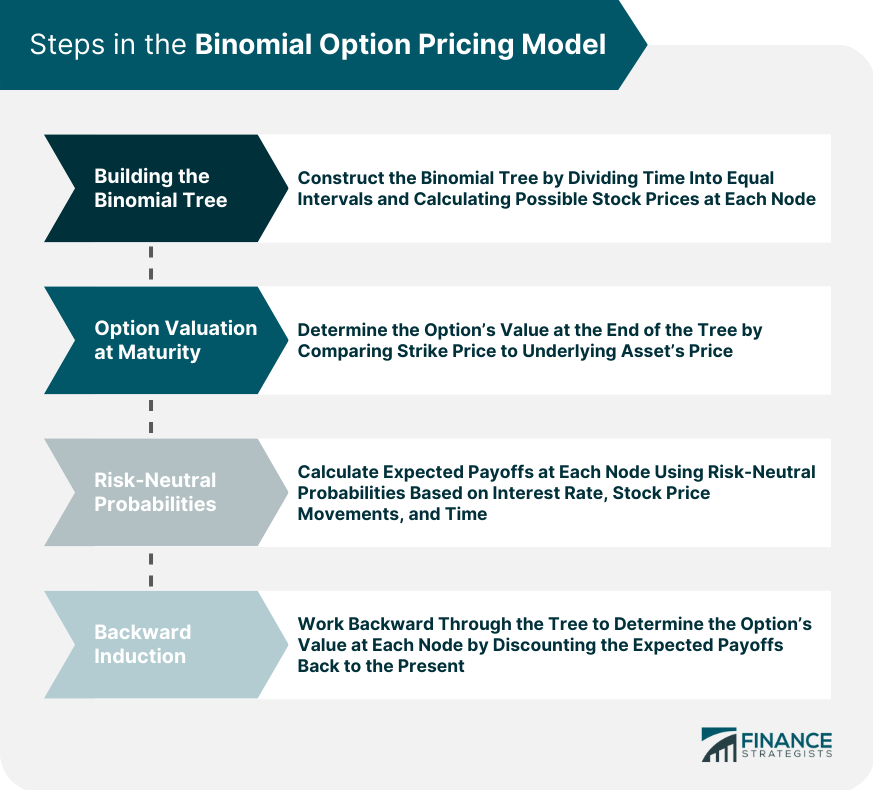
Steps in the Binomial Option Pricing Model
Building the Binomial Tree
Option Valuation at Maturity
Risk-Neutral Probabilities
Backward Induction
Types of Options Valued Using the Binomial Option Pricing Model
European Options
American Options
Exotic Options
Comparing Binomial Option Pricing Model to Other Models
Black-Scholes Model
Monte Carlo Simulation
Finite Difference Method
Practical Applications and Limitations of the Binomial Option Pricing Model
Industry Use
Impact on Financial Decision-Making
Limitations and Criticisms
Conclusion
Binomial Option Pricing Model FAQs
The binomial option pricing model is a mathematical model that calculates the theoretical value of an option by considering various parameters such as time to expiration, strike price, and underlying asset price.
The binomial option pricing model works by dividing the time to expiration into multiple time intervals, assuming that the underlying asset price can either increase or decrease during each interval, and then calculating the probability of each outcome.
The binomial option pricing model is easy to understand and implement, can handle complex options with multiple possible outcomes, and can be adjusted for different types of market conditions.
The binomial option pricing model assumes that the underlying asset price can only increase or decrease during each interval, and may not be as accurate for options with long maturities or high volatility.
The binomial option pricing model is commonly used for pricing American-style options, calculating the implied volatility of options, and valuing real options in business and investment analysis.
True Tamplin is a published author, public speaker, CEO of UpDigital, and founder of Finance Strategists.
True is a Certified Educator in Personal Finance (CEPF®), author of The Handy Financial Ratios Guide, a member of the Society for Advancing Business Editing and Writing, contributes to his financial education site, Finance Strategists, and has spoken to various financial communities such as the CFA Institute, as well as university students like his Alma mater, Biola University, where he received a bachelor of science in business and data analytics.
To learn more about True, visit his personal website or view his author profiles on Amazon, Nasdaq and Forbes.















