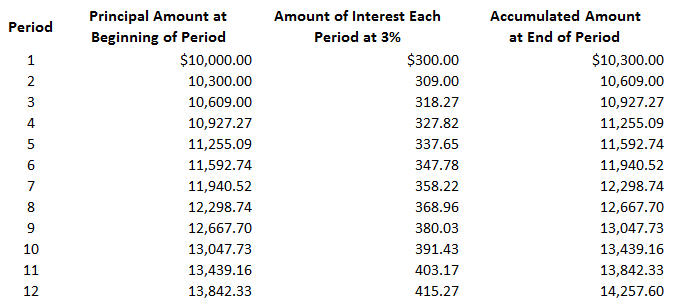
Interest is payment for the use of money for a specified period of time. Interest can be calculated on either a simple or a compound basis. The distinction between the two is important because it affects the amount of interest earned or incurred. Simple interest means that the interest payment is computed on only the amount of the principal for one or more periods. That is, if the original principal of the note is not changed, the interest payment will remain the same for each period. In this formula, the variables are defined as follows: For example, if you invest $10,000 at 12% interest for 3 years, your yearly interest income will be $1,200 ($10,000 x 0.12). The total interest earned over the 3 years would be $3,600, and you would eventually receive $13,600 ($10,000 + $3,600). Specifically: I = Pin I = $10,000 x 0.12 x 3 I = $3,600 Compound interest means that interest is computed on the principal of the note plus any interest that has accrued to date. In other words, when compound interest is applied, the accrued interest of that period is added to the amount on which future interest is to be computed. Therefore, through compounding, interest is earned or incurred not only on the principal but also on the interest left on deposit. To demonstrate the concept of compound interest, assume that the interest in the previous example is now compounded annually rather than on a simple basis. As the following table shows, in this case, the total interest income will be $4,049.28 rather than the $3,600 calculated for the simple interest case. During year 1, interest income is $1,200 (or 12%) of $10,000. Because the interest is compounded, it is added to the principal to determine the accumulated amount of $11,200 at the end of the year. Interest in year 2 is, therefore, $1,344.00 (or 12%) of $11,200, and the accumulated amount at the end of year 2 is now $12,544.00. The interest and accumulated amount at the end of year 3 are calculated in the same way. The formulas used to compute the compound amount and compound interest are shown below. The variables in this formula are defined as follows: Compound interest = Compound amount - Principal amount TD Bank has issued a loan of $2,000 to a sole proprietor for a period of 5 years at an interest rate of 7%. The interest is compounded annually. Required: Compute the compound amount and compound interest. Calculation of Compound Amount: A = P (1 + i)n A = $2,000 (1 + 7%)5 A = $2,000 (1 + 0.07)5 A = $2,000(1.07)5 A = $2,000 (1.40) A = $2,800 Calculation of Compound Interest: Compound interest = Compound amount - Principal amount = $2,800 - $2,000 = $800 Interest can be compounded as often as the lender desires. The more often interest is compounded, the faster it will increase. For example, many savings and loan institutions compound interest daily. This means that interest is calculated on the beginning balance of your account on each day. This interest is then added to the accumulated amount to determine the base for the next day's interest calculation. Clearly, this is more advantageous than if interest is compounded yearly. When calculating interest that is compounded more than annually, it is quite easy to make the necessary adjustments. If interest is compounded more often than annually, there is more than one interest period each year. For example, if interest is compounded quarterly, there are four interest periods in each year. In our example of a 3-year investment, there would be 12 interest periods if interest were compounded quarterly. But the interest rate that is stated in annual terms must be reduced accordingly. Thus, instead of using an interest rate of 12% in our example, the interest rate would be 3% each quarter. As a general rule, the annual interest rate is divided by the number of compounding periods to determine the proper interest rate for each period. If interest is compounded quarterly in the previous example of an investment of $10,000 at 12%, it will equal $4,257.60, and the total amount of the investment will grow to $14,257.60. This is shown in the following table: Thus, in this straightforward example, the total interest increases by $208.32 (from $4,049.28 to $4,257.60) when interest is compounded quarterly instead of annually.Simple Interest
Formula For Simple Interest
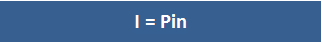
Example
Compound Interest
Example

Formulas For Compound Amount and Compound Interest
Compound Amount Formula

Compound Interest Formula
Example
Solution
Interest Compounded More Often Than Annually
Simple vs Compound Interest FAQs
Simple interest is an investment where the interest you earn does not change throughout the term of the investment. This is because there are no added funds to your initial investment during the term of an investment, so how much money your initial investment earns stays constant.
The formula used to compute simple interest is:I = PinIn this formula, the variables are defined as follows:I = Simple interest in dollarsP = Principal amounti = Interest raten = Number of periods
Compound interest is an investment where the amount of the return on your initial investment is added to that initial investment and then earns interest. A compounding period is any time interval when this process occurs, whether it be each day, each quarter, or each year.
The formula used to compute compound interest is:Compound interest = Compound amount – Principal amount
The main difference is how the return on your initial investment is paid. Simple interest means that you earn a flat percentage of your initial investment for each period, while compound interest means that you earn both principal and interest for each period. Therefore, if an investment compounds more often than annually, the return you earn will be more than what you would earn with simple interest.
True Tamplin is a published author, public speaker, CEO of UpDigital, and founder of Finance Strategists.
True is a Certified Educator in Personal Finance (CEPF®), author of The Handy Financial Ratios Guide, a member of the Society for Advancing Business Editing and Writing, contributes to his financial education site, Finance Strategists, and has spoken to various financial communities such as the CFA Institute, as well as university students like his Alma mater, Biola University, where he received a bachelor of science in business and data analytics.
To learn more about True, visit his personal website or view his author profiles on Amazon, Nasdaq and Forbes.