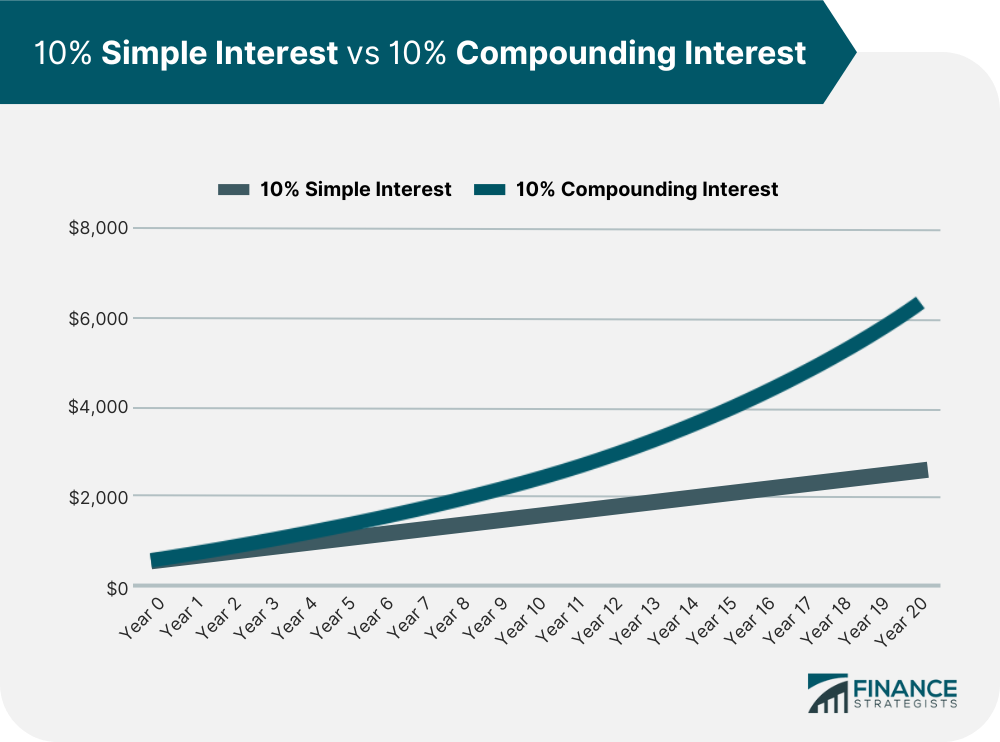
When interest is compounding, it means that when the next interest period arrives, it takes into account the total balance, rather than just the principal. For example, a $100 loan at 5% interest compounded annually will accrue a balance of $105 after one year. The next year, however, instead of taking 5% of $100, the interest will be applied to the total $105, making a new balance $110.25. The next year the interest will be applied to that $110.25, and so on for the whole length of the loan. This is different from simple interest in which a consistent amount of money, derived from a percentage of the principal, is paid to the holder of the loan periodically. Because the same interest rate will be applied to an increasingly large balance, the growth rate will be exponential. This means that the difference between compounding interest and simple interest will be minor over a short time (in the above example, only a $0.25 difference after two years) but will grow more and more quickly as time goes on. This also means that compounding interest is more sensitive to high-interest rates since that will speed the growth even more, as well as extended time periods, which allow the balance more room to grow. Typically, compounding interest works for the benefit of investors who see compounding return, but works against borrowers who have to pay off an exponentially growing loan balance. Furthermore, more frequent compounding periods benefit the lender, since they guarantee that the balance will compound as many times as possible before the balance is paid. Less frequent periods benefit the borrower since it gives more opportunity to pay back the loan before the next interest payment period. Calculating how much interest a balance will accrue in a compounding environment uses the formula X = P [ ( 1 + i ) n - 1 ] where P is the principal, i is the nominal interest expressed as a decimal, and n is the number of periods the interest will be compounded. X will be the dollar amount of interest that will be added to the principal. Let's reexamine the above example: a $100 loan at 5% interest, compounded annually, say for 3 years. The formula would look like this. X = 100 [ ( 1 + 0.05 ) 3 - 1 ] Solving for X shows that after three years, the interest accrued on the loan will be $15.76 for a total balance of $115.76. Remember that, were this loan to use simple interest, the balance would only be $115. Compounding interest doesn't only apply to loans; it can apply to investments as well. Compound Annual Growth Rate, or CAGR, is a metric used to determine the return over time of an investment in a compounding environment. CAGR is useful for estimating the expected growth of an investment portfolio over a period of years, which can be useful information when planning for goals like saving for college retirement. It can also be used to gauge how well a portfolio or fund manager is performing relative to the market returns. For example, if a market index provided total returns of 5% over a five-year period, but a fund manager has only provided 4%, then they are underperforming relative to the market. Likewise, if the manager returns 6%, then they are outperforming the market.Define Compound Interest in Simple Terms
How to Calculate Compound Interest
Compound Annual Growth Rate (CAGR)
Compound Interest FAQs
When interest is compounding, it means that when the next interest period arrives, it takes into account the total balance, rather than just the principal.
The formula for calculating compound interest is X=P[(1+i)n-1] where P is the principal, i is the nominal interest expressed as a decimal, and n is the number of periods the interest will be compounded.
Simple interest only pays interest on the principal balance, while compound interest also pays interest on the interest that is earned.
Because the same interest rate will be applied to an increasingly large balance, the growth rate will be exponential.
Compounding interest doesn’t only apply to loans; it can apply to investments as well. Compound Annual Growth Rate, or CAGR, is a metric used to determine the return over time of an investment in a compounding environment.
True Tamplin is a published author, public speaker, CEO of UpDigital, and founder of Finance Strategists.
True is a Certified Educator in Personal Finance (CEPF®), author of The Handy Financial Ratios Guide, a member of the Society for Advancing Business Editing and Writing, contributes to his financial education site, Finance Strategists, and has spoken to various financial communities such as the CFA Institute, as well as university students like his Alma mater, Biola University, where he received a bachelor of science in business and data analytics.
To learn more about True, visit his personal website or view his author profiles on Amazon, Nasdaq and Forbes.















